[Basic quantitative analyses of medical examinations]

 Andreas M?ltner ¹
Dieter Schellberg ²
Jana J?nger <sup>1

1</sup> Ruprecht-Karls-Universit?t Heidelberg, Kompetenzzentrum f?r Pr?fungen in der Medizin - Baden-W?rttemberg, Heidelberg, Deutschland
² Universit?tsklinikum Heidelberg, Psychosomatische und Allgemeine Klinische Medizin, Heidelberg, Deutschland

Abstract

The evaluation steps are described which are necessary for an elementary test-theoretic analysis of an exam and sufficient as a basis of item-revisions, improvements of the composition of tests and feedback to teaching coordinators and curriculum developers. These steps include the evaluation of the results, the analysis of item difficulty and discrimination and - where appropriate - the corresponding evaluation of single answers. To complete the procedure, the internal consistency is determined, which makes an estimate of the reliability and significance of the examination.

---

---

Einleitung

Wozu dient die quantitative Analyse einer Pr?fung?

Nach der neuen ?AppO werden im Abschlusszeugnis einer Universit?t mehr als 30 Noten aufgef?hrt [18]. Doch was sagen diese Noten ?berhaupt aus? Wer als Klinikleiter auf ein Zeugnis blickt, fragt sich, ob jemand mit einer Eins in einem bestimmten Fach wirklich mehr wei? oder kann als jemand mit einer Drei. Studierende mit einer guten Note wollen mit dieser auch re?ssieren, die mit einer schlechten fragen sich, ob sie nicht - aus welchen Gr?nden auch immer - ungerecht behandelt worden sind. Von den letzteren werden m?glicherweise einige versuchen, Pr?fungen juristisch anzufechten, und - nach der Einf?hrung von Studiengeb?hren - eventuell sogar auf Schadensersatz dringen. Ob es dann ausreichen wird, auf die Bem?hungen zur Erstellung inhaltlich angemessener und aussagekr?ftiger Pr?fungen hinzuweisen, ist fraglich, letztendlich ist man erst dann auf der sicheren Seite, wenn f?r die Einhaltung eines Mindeststandards der Pr?fungsqualit?t auch ein Nachweis erbracht werden kann. Solch ein Nachweis bedarf jedoch einer quantitativen Analyse der Pr?fungsresultate.

Neben solchen externen gibt es aber auch gen?gend andere Gr?nde f?r die quantitative statistische Analyse von Pr?fungen: So ist etwa der Erfolg einer guten Pr?fungsvorbereitung nie garantiert, es wird immer wieder vorkommen, dass einzelne Fragen oder Aufgaben sich erst w?hrend oder nach der Pr?fung als zu schlecht konzipiert erweisen. Entf?llt eine Kontrolle, kann man Schwachstellen einer Pr?fung nicht identifizieren und damit auch nicht aus seinen Fehlern lernen. Letztendlich w?rde dies die Aufgabe des Anspruchs bedeuten, zuverl?ssig und gut zu pr?fen.

Individuell wird mit einer Pr?fung die Leistungsf?higkeit eines Studierenden beurteilt, bezogen auf die Gruppe aller Pr?fungskandidaten pr?ft sie den Lehrerfolg. Kann die Mehrzahl der Studierenden eine Aufgabe nicht bew?ltigen, so wurden die zur L?sung notwendigen Kenntnisse oder Fertigkeiten offensichtlich nicht hinreichend vermittelt, dies sollte zu Konsequenzen hinsichtlich der Lehre f?hren. F?r eine gute R?ckmeldung von Pr?fungsergebnissen an die Lehrenden ist jedoch eine differenzierte und klare Ergebnispr?sentation notwendig, f?r die eine fundierte Pr?fungsauswertung ben?tigt wird.

Dies sind alles gute Gr?nde f?r eine quantitative Analyse von Pr?fungen. Wie geht man aber bei der Auswertung praktisch vor? Die nachfolgenden Ausf?hrungen sollen hierzu eine Reihe von Hinweisen geben. Hinsichtlich einer detaillierten testtheoretischen Pr?fungsauswertung sind diese sicherlich nicht vollst?ndig, in der Praxis wird mit dem vorgestellten Vorgehen aber die ?berwiegende Zahl von Problemen bei Aufgaben und Pr?fung quantitativ erfasst und damit die notwendige empirische Basis einer zielgerichteten Revision von Aufgaben und Pr?fungszusammenstellung gebildet. Schlie?lich beinhalten sie bei guten Pr?fungen auch den Nachweis ihrer Zuverl?ssigkeit (Reliabilit?t). Nicht angestrebt ist im Weiteren eine Darstellung der testtheoretischen Hintergr?nde, hierf?r sei auf die umfangreiche Fachliteratur zu diesem Thema verwiesen (z. B. [7], [11] [12]). Weiterhin sei angemerkt, dass sich die hier beschriebenen Verfahren im Rahmen der klassischen Testtheorie bewegen, deren Hauptziel in einer m?glichst guten Differenzierung der Pr?fungskandidaten besteht. Dies bedeutet nicht, dass wir der klassischen Testtheorie den Vorzug vor einer kriteriumsorientierten Leistungsmessung geben, viele der dort entwickelten Vorgehensweisen behalten jedoch auch in diesem Kontext ihren Wert.

?bersicht

In den folgenden Abschnitten wird ein strukturiertes Vorgehen f?r eine quantitative Pr?fungsauswertung vorgeschlagen, welches aus den Hauptpunkten Ergebnis?bersicht, Analyse der Aufgabenschwierigkeiten, der Trennsch?rfen und schlie?lich der Zuverl?ssigkeit (Reliabilit?t) besteht. Voraussetzung dabei ist, dass die Bewertung der Pr?fung durch die Vergabe von "Punkten" f?r Einzelaufgaben erfolgt und die Gesamtbeurteilung an Hand der Summe dieser Punkte erfolgt (der Einfachheit halber sei angenommen, dass die minimale Punktzahl einer Aufgabe mit 0 angenommen ist, Aufgaben mit m?glichen "Strafpunkten" werden nicht in Betracht gezogen). Unter "Aufgaben" k?nnen Fragen einer Klausur, Stationen eines OSCE-Parcours, zu verschiedenen Zeitpunkten durchgef?hrte klinische Beobachtungen etc. verstanden werden, die Vorgehensweise ist in allen F?llen die gleiche. Neben einer "generellen" Auswertung hinsichtlich Schwierigkeit und Trennsch?rfe kann bei Aufgaben, bei denen die Antwort- oder Reaktionsm?glichkeiten in eine begrenzte Zahl von Kategorien eingeteilt werden k?nnen, eine detaillierte Antwortanalyse erfolgen. Bekanntestes Beispiel solcher Aufgaben sind Multiple-Choice-Aufgaben, in denen z. B. lediglich f?nf Antwortm?glichkeiten vorgegeben sind. Detaillierte Analysen sind jedoch nicht nur auf solche "geschlossenen" Aufgaben (synonym: Aufgaben mit gebundener Beantwortung) beschr?nkt, sondern k?nnen auf alle Aufgaben angewandt werden, in denen die "L?sungsversuche" (richtige wie falsche) der Aufgabe von vorneherein oder auch erst post hoc sinnvoll kategorisierbar sind.

Den Abschluss bilden einige allgemeine Anmerkungen zu den Themen Objektivit?t, Validit?t und Reliabilit?t nicht-homogener Pr?fungen, die ?ber das hier gesteckte Ziel, den Inhalt einer grundlegenden Pr?fungsauswertung darzustellen, hinausf?hren.

Auswertungsschritte

Gesamtergebnis

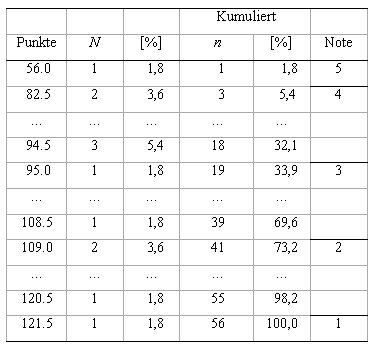
Vorrangig interessiert alle Beteiligte selbstverst?ndlich das Gesamtergebnis, das in Form einer tabellarischen Auflistung der H?ufigkeiten der Gesamtpunktzahlen (siehe Tabelle 1) und als Histogramm (siehe Abbildung 1) dargestellt wird. Erg?nzt werden k?nnen diese durch die Angabe der Bestehensgrenzen und des Notenschl?ssels. Im aufgef?hrten Beispiel wird von einer Benotung an Hand einer klassischen Notenskala von 1 bis 5 ausgegangen, je nach Studien- oder Pr?fungsordnung sind Modifikationen, etwa bei Vergabe von Zwischen- oder Dezimalnoten, m?glich.

Die visuelle Inspektion des Histogramms gibt einen meist ausreichenden ?berblick ?ber Punkte- und Notenverteilung. Unserer Erfahrung nach sind Pr?fungsergebnisse meist nur in grober Ann?herung symmetrisch verteilt; bei auff?lligen Abweichungen, wie z. B. mehrgipfligen Verteilungen, sollte eine ?berpr?fung der Ausgangsdaten erfolgen. H?ufig zu beobachten sind Ausrei?er nach unten, also Studierende mit auff?llig wenigen Punkten. Das sind oft Pr?fungsabbrecher (ob sie tats?chlich den Raum verlassen haben oder z. B. nur noch entmutigt vor ihrem Fragebogen sitzen ist diesbez?glich egal), von Bedeutung f?r die statistische Analyse sind sie deshalb, weil sie bei der Analyse von Trennsch?rfen und Reliabilit?t zu verzerrten Ergebnissen f?hren k?nnen und deshalb bei einer ernstzunehmenden Analyse von weiteren Berechnungen ausgeschlossen werden sollten (selbstverst?ndlich muss auch bei diesen die Korrektheit der Angaben ?berpr?ft werden, triviale Fehler bei der Dateneingabe wie das Vergessen einer ganzen Aufgabe oder Aufgabengruppe sind h?ufiger als man vermutet). Die Identifikation von Ausrei?ern kann mit objektiven statistischen Methoden erfolgen, wobei zu beachten ist, dass die Normalverteilungsannahme f?r die Punkteverteilung h?ufig nicht erf?llt ist, (vgl. z. B. [17]), im Allgemeinen ist jedoch die "optische" Identifikation ausreichend. [Tab. 1] [Abb. 1]

Teststatistische Analyse von Aufgaben

1. Aufgabenschwierigkeit

Nach dem ?berblick ?ber die Gesamtergebnisse der Pr?fung erfolgt die Untersuchung der Aufgabenschwierigkeiten. In der Literatur wird meist der Begriff "Itemschwierigkeit" ("item difficulty") verwendet, der auf dessen Herkunft aus der psychologischen Testtheorie verweist. Da er aber auf jede Form von mit Punkten bewerteten Aufgaben ?bertragbar ist, soll hier der etwas allgemeinere Begriff "Aufgabe" verwendet werden.

Definiert ist die Aufgabenschwierigkeit als die mittlere bei dieser Aufgabe erreichte Punktzahl (bei Aufgaben, f?r die bei korrekter Beantwortung genau ein Punkt und ansonsten kein Punkt vergeben wird, stimmt die Schwierigkeit mit der relativen Anzahl von Studenten, die richtig geantwortet haben, ?berein). Hohe Werte charakterisieren demnach eher leichte, niedrige Werte eher schwere Aufgaben, weshalb - semantisch korrekter - manchmal auch die Bezeichnung "item easiness" zu finden ist.

Zu beachten ist, dass die Schwierigkeit keine Eigenschaft der Aufgabe per se darstellt, sondern immer in Bezug auf die gepr?fte Stichprobe oder eine Pr?fungspopulation zu sehen ist. Die gleiche Aufgabe in einer Pr?fung nach einem Einf?hrungskurs besitzt sicherlich eine andere Schwierigkeit als bei Examenskandidaten. Bei Pr?fungen, in denen bei den Aufgaben unterschiedliche Punktzahlen vergeben werden, ist die so definierte Aufgabenschwierigkeit zum Vergleich nicht geeignet, man verwendet stattdessen die "normierte Aufgabenschwierigkeit" P = /max, die den relativen (oder den prozentualen) Anteil an der maximal erreichbaren Punktzahl max einer Aufgabe angibt (beachte: nicht der maximal erreichten Punktzahl in der Pr?fung). Aufgaben mit einem Wert von P = 1 sind solche, bei denen immer die volle Punktzahl erreicht wurde, bei P = 0,5 wurde im Mittel die H?lfte der erreichbaren Punkte erzielt, P = 0 erh?lt man bei Aufgaben, bei denen niemand einen Punkt erreicht hat.

F?r die Pr?fungsersteller ist dringend zu empfehlen, schon w?hrend der Vorbereitung und w?hrend des Reviewprozesses eine grobe Einsch?tzung der Aufgabenschwierigkeiten (erwartete Schwierigkeit ) zu geben. Dies dient dazu, den Erwartungshorizont hinsichtlich der L?sbarkeit der Aufgaben niederzulegen. Ein Vergleich der erwarteten Punktesummen mit den anzusetzenden Notengrenzen erlaubt eine grobe Vorstellung von den Endergebnissen, manche Pr?fung mit ?berraschend hohen Durchfallquoten h?tte dadurch vermieden werden k?nnen. Dies ?hnelt in gewisser Hinsicht dem Vorgehen beim "Standard-Setting", im Unterschied zu diesem wird jedoch nicht festgelegt, welche Mindestpunktzahl von einem Studenten zum Bestehen erwartet (im Sinne von "gefordert") wird, sondern welche Punktzahl im Mittel erreicht wird.

Richtwerte

Als Richtwert f?r die Aufgabenschwierigkeit wird in der Literatur der Bereich von etwa 0,4 bis 0,8 empfohlen. Aufgaben mit h?heren Werten als 0,8 gelten als zu leicht, aus Sicht der klassischen Testtheorie, in der vor allem der Aspekt einer guten Differenzierung betont wird, sind solche Aufgaben in Hinblick auf die Pr?fungs?konomie ?berfl?ssig (Warum sollte gefragt werden, was ohnehin fast jeder beherrscht?). Im Sinne einer kriteriumsorientierten Pr?fung ist es jedoch durchaus sinnvoll, wichtige basale Fertigkeiten oder Kenntnisse in einer Pr?fung unabh?ngig von ihrer erwarteten Schwierigkeit abzufragen. F?r zu schwere Aufgaben gilt ?hnliches. Die Asymmetrie (0,4-0,8 statt 0,2-0,8) ist im Wesentlichen damit begr?ndet, dass zu viele schwere Aufgaben in Pr?fungen demotivierend wirken.

Die Auflistung der Aufgabenschwierigkeiten erfolgt am besten in einer Tabelle, etwa in der Form von Tab. 2 (s. unten: "Beispiele“), in der die erwarteten und tats?chlichen mittleren erreichten Punktzahlen numerisch aufgef?hrt sind. Hilfreich ist eine zus?tzliche graphische Darstellung der erwarteten und tats?chlichen Aufgabenschwierigkeiten P = /max, da hier deutliche Abweichungen dieser Werte wie auch sehr leichte und schwere Aufgaben leicht zu identifizieren sind.

Von Interesse sind nat?rlich alle Aufgaben, bei denen deutliche Diskrepanzen zwischen Erwartung und Realit?t bestehen, sei es, dass sie unerwartet schwer oder unerwartet leicht sind. F?r diese ist nach Erkl?rungen zu suchen, sie k?nnen in mangelhaften Aufgabenstellungen begr?ndet sein (etwa den Distraktoren bei Multiple-Choice-Items, unklare Anforderungen bei OSCE-Stationen), oder in fehlerhaften Vorstellungen ?ber die vermittelten Lerninhalte. Ein solches Vorgehen ist zugegebenerma?en ein m?hseliges Unterfangen, letztendlich jedoch lohnenswert, da es einerseits eine empirische Basis f?r Aufgabenrevisionen liefert und zum anderen die Grundlage f?r die Feedbackschleife von Pr?fung zu Curriculumsentwicklung schafft.

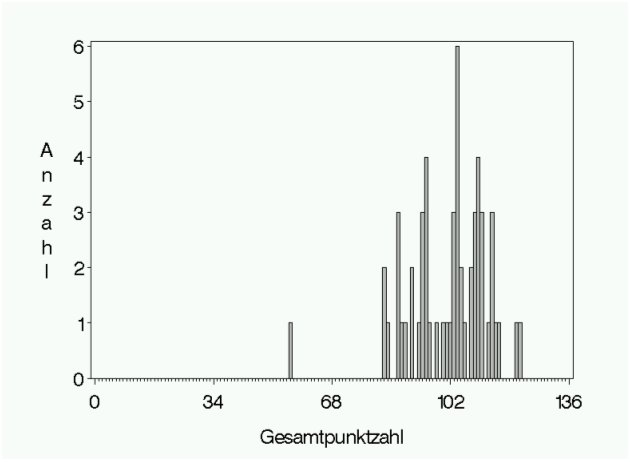
Zur zusammenfassenden Darstellung der normierten Aufgabenschwierigkeiten dient deren Histogramm (siehe Abbildung 2 [Abb. 2]). Entsprechend den angegeben Richtwerten sollten diese vor allem im Bereich von 0,4 bis 0,8 streuen, bei feststehenden Bestehensgrenzen (z. B. bei ?bernahme der 60%-Grenze der ?AppO) ist diese zu ber?cksichtigen und deshalb mehr leichte Aufgaben in der Pr?fung zu verwenden (in erster N?herung entspricht die Note, die f?r die mittlere erreichte Punktzahl vergeben wird auch dem Notendurchschnitt).

Vorsicht ist geboten, wenn ein Teil der Pr?fungskandidaten auf Grund der beschr?nkten Pr?fungszeit nicht alle Aufgaben bearbeiten konnte, die daraus folgende Bewertung mit 0 Punkten ist in diesen F?llen nicht auf deren Schwierigkeit zur?ckzuf?hren. Auf Grund von Zeitmangel nicht bearbeitete Aufgaben sind bei diesen Pr?flingen von der Auswertung auszuschlie?en. Im speziellen Fall von Multiple-Choice-Klausuren ist dies in der Praxis schwierig zu erfassen, da bei knapper Zeit Pr?fungskandidaten verbliebene Fragen mit der Hoffnung auf Zufallstreffer "blind" kreuzen, in den meisten Pr?fungen sollte jedoch ohnehin hinreichend Zeit f?r die Bearbeitung aller Aufgaben zur Verf?gung stehen.

2. Trennsch?rfe

Damit eine Aufgabe in einer Pr?fung Sinn macht, muss sie zwischen guten und schlechten Pr?fungskandidaten unterscheiden k?nnen (vgl. jedoch hierzu auch Abschnitt "Erh?hung der Reliabilit?t von Pr?fungen"). Besitzt man ein messbares Au?enkriterium f?r "gut" und "schlecht", so wird die Korrelation der bei einer Aufgabe erreichten Punktzahl mit diesem Kriterium als externe (Item-)Validit?t bezeichnet. Im Rahmen einer Pr?fung steht ein solches Au?enkriterium im Allgemeinen jedoch nicht zur Verf?gung, weshalb man sich damit behilft, das Gesamtergebnis der Pr?fung (also die Punktesumme) als Kriterium zu verwenden. Dabei wird angenommen, dass bei inhaltlich ad?quater Wahl der Aufgaben diese "im Gro?en und Ganzen" ein geeignetes Kriterium f?r "besser" oder "schlechter" darstellen. Den Grad der ?bereinstimmung von Aufgabe mit Gesamtpunktzahl bezeichnet man als Trennsch?rfe.

Sie ist die "F?higkeit" einer Aufgabe zwischen guten und schlechten Pr?fungskandidaten zu unterscheiden. Erreichen Kandidaten mit einer hohen Punktzahl in der gesamten Pr?fung bei einer Aufgabe relativ viele Punkte, Kandidaten mit niedriger Gesamtpunktzahl nur wenige, so besitzt sie eine hohe Trennsch?rfe. Eine Aufgabe mit Trennsch?rfe um 0 wird von guten wie schlechten Pr?fungskandidaten gleich gut oder schlecht beantwortet. Denkbar sind auch Aufgaben mit negativer Trennsch?rfe, diese sind solche, bei denen "paradoxerweise" gute Kandidaten wenig, schlechte Kandidaten hingegen viele Punkte erreichen.

Zur Charakterisierung der G?te, mit der eine Aufgabe gute und schlechte Kandidaten trennt, werden verschiedene Indizes verwendet (man beachte, dass in der Literatur die Terminologie nicht immer einheitlich ist).

Diskriminationsindex

Das anschaulichste Ma? ist der Diskriminationsindex D ("index of discrimination" [7], [10]). Dieser beruht auf einer Aufteilung der Pr?flinge in Gruppen "guter" und "schlechter" Kandidaten an Hand ihrer erreichten Gesamtpunktzahlen. Der Index ist dann definiert als Differenz der normierten mittleren Schwierigkeit der Gruppe der "guten" und der der "schlechten" Kandidaten. In der urspr?nglichen Version von Kelley [10] wird dabei eine Einteilung der Pr?fungskandidaten am unteren und oberen 27%-Perzentil in drei Gruppen vorgenommen (D ist damit die Differenz der 27% besten zu den 27% schlechtesten). Bezeichnet die mittlere erreichte normierte Punktzahl der Gruppe der besten Pr?fungskandidaten und die der schlechtesten, so ist D = - .

Es gibt verschiedene Varianten zu D, so kann die Gruppeneinteilung an den Terzilen (unteres und oberes 33%-Perzentil statt der 27%-Perzentile) oder eine Einteilung in nur zwei Gruppen am Median erfolgen. Unseres Erachtens ist eine Einteilung in drei Gruppen (gut/mittel/schlecht) vorzuziehen, ob diese an den 33%- oder den 27%-Perzentilen erfolgt ist unwesentlich. Trennt die Aufgabe gut, so ist die Differenz D offensichtlich gro?, trennt sie schlecht, liegt sie nahe bei 0, negative D erh?lt man bei den bereits erw?hnten paradoxen Antwortmustern.

(Die Zahl von 27% ist darauf zur?ckzuf?hren, dass D urspr?nglich als Schnellsch?tzung f?r eine Korrelation entwickelt worden ist und eine Aufteilung an den 27%-Perzentilen gewisse Optimalit?tseigenschaften aufweist. Als Korrelationssch?tzung ist D jedoch an zus?tzliche Voraussetzungen gebunden; wir behandeln D als eigenst?ndiges Ma?.)

Ein Nachteil von D besteht darin, dass bei der Aufteilung in gute und schlechte Pr?fungsabsolventen an Hand der Gesamtpunktzahl, der Punktwert, der bei der betrachteten Aufgabe erreicht wird, diese Aufteilung mit beeinflusst. Es ist deshalb angebracht, die Einteilung auf Basis der erreichten Punktsumme aller anderen Aufgaben vorzunehmen (korrigierter Diskriminationsindex D'). Bei Pr?fungen, die aus vielen Aufgaben bestehen, ist der Unterschied zwischen D und D' vernachl?ssigbar, jedoch sollte die Korrektur z. B. bei OSCE-Pr?fungen, die selten mehr als 20, meist jedoch weniger Stationen umfassen, unbedingt durchgef?hrt werden.

Bei der Ergebnisdarstellung in Tab. 2 (s. unten: "Beispiele") sind die mittleren erreichten Punktzahlen in den Gruppen mit aufgef?hrt, D' ergibt sich optisch als Unterschied zwischen der Schwierigkeit in der Gruppe "gut" und der Gruppe "schlecht".

Korrelationsma?e

H?ufiger als D werden Korrelationsma?e zur Charakterisierung der Trennsch?rfe verwendet, insbesondere der ?bliche Korrelationskoeffizient r nach Pearson-Bravais. Die Trennsch?rfe ist dann die Korrelation der in der Aufgabe erreichten Punktzahlen mit den Gesamtpunkten in der Pr?fung. Bei "unsch?n" verteilten Daten (stark schiefe Verteilungen, Ausrei?er) sind nicht-parametrische Korrelationskoeffizienten (z. B. Spearmans oder Kendalls ) als Kennzahlen auf Grund ihrer geringeren Abh?ngigkeit von Extremwerten oft besser geeignet, nach der in Abschnitt 2 beschriebenen Ausrei?erbereinigung sind die Unterschiede zu r aber eher gering.

Wie bei D' sollte der in der betrachteten Aufgabe erreichte Punktwert nicht bei der Gesamtpunktzahl ber?cksichtigt werden, analog ist die korrigierte Trennsch?rfe r' (oder ) definiert als Korrelation der erreichten Punktzahl mit der Summe der Punkte in allen anderen Aufgaben (die Korrektur wird auch als "part-whole-correction" bezeichnet).

Als Standardvorgehen ist die Verwendung der korrigierten Pearson-Korrelation r' zu empfehlen und diese auf ?bereinstimmung mit einer nicht-parametrischen Korrelation, z. B. nach Spearman, zu pr?fen. Bei auff?lligen Differenzen ( > 0, 20) sollte eine Nachkontrolle bzgl. Ausrei?er erfolgen.

Unterschiedliche Bedeutung von D und r

Die Koeffizienten r und D unterscheiden sich insofern, als r eher die "Sch?rfe" der Trennung von guten und schlechten Kandidaten angibt, D hingegen eher die "Gr??e" des Unterschieds. Damit repr?sentiert r die Trennsch?rfe besser; in der Praxis zeigt sich jedoch meist, dass das anschaulichere Ma? D zur Aufgabenbeurteilung im Allgemeinen ausreichend ist.

Aus mathematisch-statistischer Sicht sind Korrelationsma?e als Kenngr??en der Trennsch?rfe dem "Index of discrimination" D vorzuziehen, da sie die "F?higkeit" einer Aufgabe, zwischen guten und schlechten Kandidaten zu unterscheiden auch dann anzeigen, wenn bei den Bewertungen der Aufgabe in der Pr?fung nur ein Teilbereich zwischen 0 und maximal erreichbarer Punktzahl verwendet wird.

(Beispiel: Sind bei einer OSCE-Station maximal 20 Punkte zu erreichen und werden vom besten Drittel der Studierenden zwischen 19 und 20 Punkte, vom mittleren Drittel zwischen 18 und 19 und vom schlechtesten Drittel der Studierenden zwischen 17 und 18 Punkte erreicht, so ist die Trennsch?rfe gemessen mit dem Korrelationskoeffizienten r sehr gut (r 0,8), gemessen mit D jedoch eher m??ig (D 0,1).)

Richtwerte

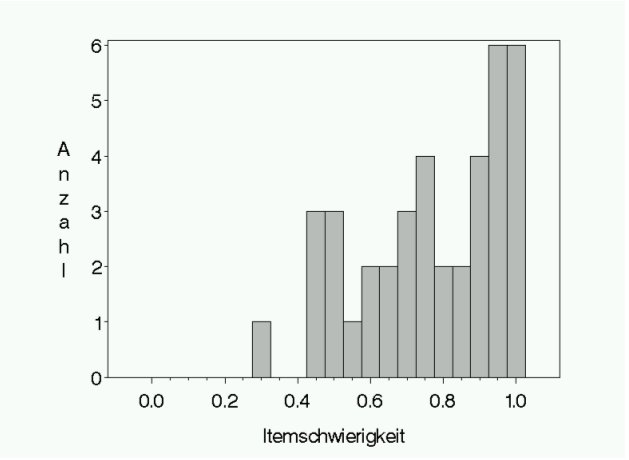
Trennsch?rfen r' von ?ber 0,3 gelten als gut und zwischen 0,2 und 0,3 als akzeptabel. Trennsch?rfen zwischen 0,1 und 0,2 k?nnen noch als marginal angesehen werden, Werte unter 0,1 sind schlecht, hier haben die bei den Aufgaben erzielten Punktzahlen kaum oder nichts mehr etwas mit "guten" oder "schlechten" Pr?fungskandidaten zu tun. Aufgaben mit negativen Trennsch?rfen wirken sich in jedem Fall sch?dlich auf die Pr?fungsgenauigkeit aus. Wie bei den Aufgabenschwierigkeiten dient ein Histogramm der Trennsch?rfen aller Pr?fungsaufgaben als zusammenfassender ?berblick (siehe Abbildung 3 [Abb. 3]).

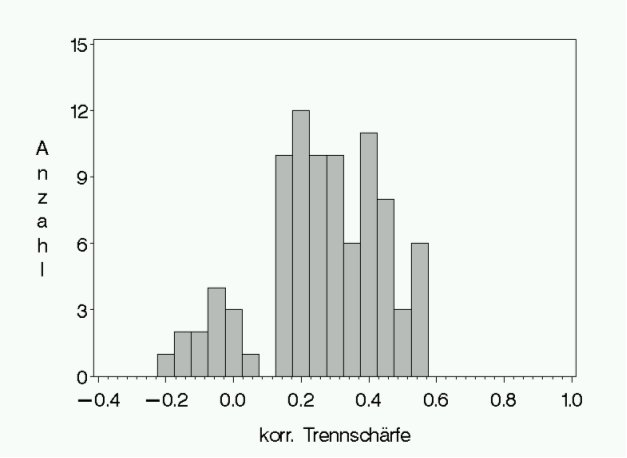
Man beachte, dass die Trennsch?rfe einer Aufgabe nicht nur von der Pr?fungspopulation abh?ngig ist (wie die Aufgabenschwierigkeit), sondern auch von der Gesamtheit aller Pr?fungsaufgaben. Wird z. B. eine Aufgabe in einer Klausur f?r Innere Medizin v?llig identisch in einer Pr?fung f?r Biochemie gestellt und beantwortet, so bleibt deren Schwierigkeit gleich, die Trennsch?rfe kann jedoch v?llig anders sein. Im Rahmen einer Pr?fung mit vielen "schlechten" Aufgaben wird auch eine "sehr gute" Aufgabe eine niedrige Trennsch?rfe aufweisen!

Beispiele

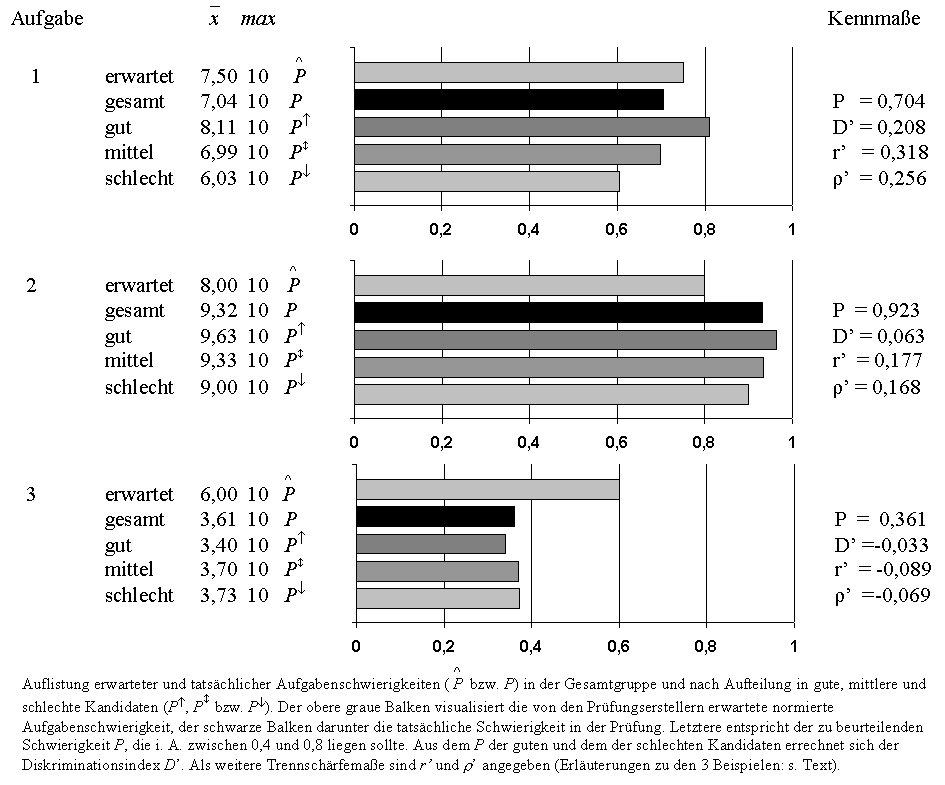
Tabelle 2 [Tab. 2] illustriert die in diesem Abschnitt beschriebene Kennma?e:

Aufgabe 1 besitzt eine Schwierigkeit von 0,704 und eine gute Trennsch?rfe (). Erwartet wurde von den Pr?fern ein Mittel von 7,5 Punkten, die Einsch?tzung liegt in der Gr??enordnung des tats?chlichen Werts. Die gute Trennsch?rfe wird durch den Diskriminationsindex ebenfalls deutlich: Die Gruppe der besten Studenten erreicht 2,08 Punkte (= ) oder 0.208 normierte Punkte mehr als die der schlechtesten.

Bei Aufgabe 2 wurden im Mittel statt der erwarteten 8 Punkte 9,32 Punkte erzielt, Aufgabe 2 ist zu leicht (P > 0, 9), sie weist zudem eine deutlich niedrigere Trennsch?rfe auf (r' = 0, 177), gute und schlechte Studenten unterscheiden sich im Mittel um 0,63 Punkte (0.063 normierte Punkte).

Aufgabe 3 ist sehr schwer (P < 0, 4) und besitzt sogar eine negative Trennsch?rfe (r' < 0), die schlechten Studenten erreichen im Mittel etwas mehr (normierte) Punkte als die guten.

Einzelantwort- oder Distraktorenanalyse

1. H?ufigkeitsanalyse der Antworten

Bei Aufgaben mit beschr?nkter Zahl m?glicher Antworten (wie z. B. Multiple-Choice-Fragen oder Long-Menu-Items) oder nachtr?glicher Klassifizierung der gegebenen Antworten ist ?ber die Aufgabenschwierigkeiten hinaus eine detailliertere H?ufigkeitsanalyse aller Antwortm?glichkeiten, also auch der falschen, von Bedeutung (im Kontext von MC-Fragen werden diese als Distraktoren bezeichnet). Sie dient bei geschlossenen Aufgaben in erster Linie zur Identifikation untauglicher Antwortalternativen, allgemein zur Feststellung, welche Art von Fehlern bei Aufgaben den Studierenden h?ufig unterlaufen (z. B. kontraindizierte Ma?nahmen bei praktischen Pr?fungen).

Paradebeispiel ist ein klassisches MC-Item vom Typ A ("Eins aus F?nf"). Die entsprechende Tabelle enth?lt alle 5 Antwortalternativen und ihre absoluten wie relativen H?ufigkeiten, in Tabelle 3 [Tab. 3] sind zwei Beispiele aufgef?hrt. Genauer zu betrachten sind hier Aufgaben, in denen eine der Falschkategorien h?ufiger gew?hlt wird als die korrekte Antwort. Hier ist nach den Gr?nden zu fragen, warum die Studierenden eine Falschantwort ?fter angeben als die richtige. Ursache daf?r ist vielfach eine unklare Abgrenzung der Fehlantwort/des Distraktors von der richtigen Antwort oder die Tatsache, dass die korrekte Antwort doch nicht eindeutig die beste Antwort ist. Weiter gibt die Tabelle Auskunft dar?ber, welche Falschkategorien/Distraktoren ?berhaupt oder wie h?ufig sie gew?hlt wurden.

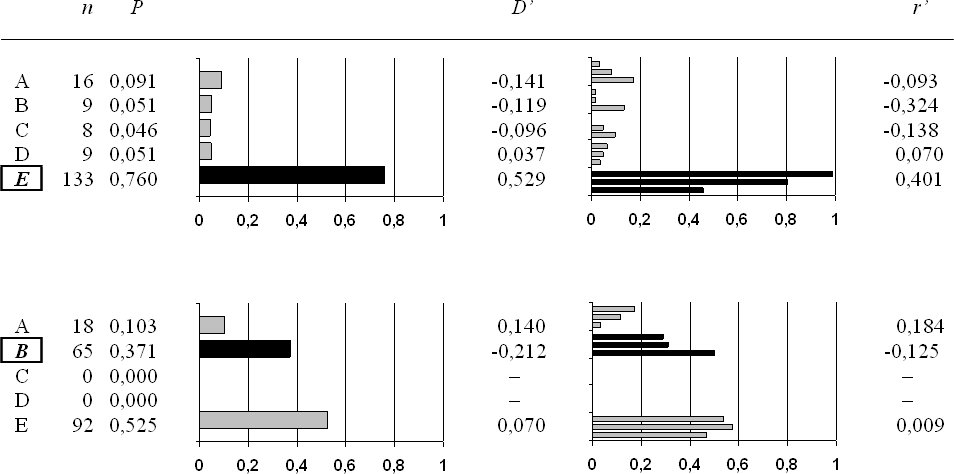
Bei geschlossenen Aufgaben mit wenigen Distraktoren ist bei nie oder nur selten gew?hlten Falschantworten zu vermuten, dass diese auch bei Unkenntnis der richtigen Antwort schon von vornherein ausgeschlossen werden k?nnen. Dadurch erh?ht sich die Wahrscheinlichkeit, die richtige L?sung zu erraten, deutlich, weshalb diese Antwortm?glichkeiten einer n?heren Pr?fung hinsichtlich ihrer Tauglichkeit zu unterziehen sind.

Erfahrungsgem?? werden bei dieser Antwortanalyse die meisten fehlerhaften Aufgaben identifiziert, die im Nachhinein eine Korrektur der Bewertungsvorgaben erforderlich machen.

2. Trennsch?rfenanalyse von Antworten/Distraktoren

Bei einer detaillierten Antwortanalyse werden analog zur Aufgabenschwierigkeit nicht nur die korrekten sondern auch die falschen Antworten (bei MC-Items: Distraktoren) ausgewertet.

(Anmerkung: Mathematisch lassen sich "Antworten" nicht mit einer Punktzahl korrelieren, man bildet vielmehr f?r jede Antwortm?glichkeit (z. B. A, B, C, D und E) eine sog. Indikator-Variable, die f?r jeden Pr?fungskandidaten den Wert 1 aufweist, falls dieser die Antwort gew?hlt hat, ansonsten den Wert 0. Die Berechnungen von Trennsch?rfema?en beziehen sich auf diese Indikator-Variablen.)

Korrekte Antwortm?glichkeiten sollten eine hohe Diskrimination aufweisen, falsche Antwortm?glichkeiten eine negative, d. h. "gute" Studierende w?hlen richtige Antworten h?ufiger und falsche Antworten seltener als schlechte Studierende. F?r korrekte Antwortm?glichkeiten gilt das im letzten Abschnitt Erw?hnte, niedrige Trennsch?rfen zeigen einen ungen?genden Zusammenhang zwischen Antwort und Gesamtscore.

Anders ist es bei den falschen Antwortm?glichkeiten, hier sind positive Trennsch?rfen auff?llig, man sollte ?berlegen, warum gute Studenten eine solche (falsche) Antwort h?ufiger w?hlen als schlechte.

Die Ergebnisdarstellung enth?lt wie bei der allgemeinen Aufgabenanalyse eine graphische Darstellung der relativen H?ufigkeiten in den drei Gruppen gut/ mittel/schlecht (s. Tab. 3).

(Man beachte, dass bei den klassischen MC-Items vom Typ A ("Eins aus F?nf") die Trennsch?rfe des Items mit der Trennsch?rfe der korrekten Antwort ?bereinstimmt, dies gilt jedoch nicht f?r alle Antwortformate. Bei Items vom Typ K' (f?r die Typenbezeichnungen von MC-Items s. [2]) sind auf eine Frage vier Ja-Nein-Alternativen zu beantworten, ein Punkt wird f?r das Item nur gegeben, wenn alle vier Antworten korrekt sind. In diesem Fall ist die Trennsch?rfe des Gesamtitems etwas anderes als die Trennsch?rfen der korrekten Antworten auf einzelnen Unterfragen.)

Reliabilit?t

1. Bedeutung der Reliabilit?t

Die Reliabilit?t bezeichnet die Zuverl?ssigkeit oder Reproduzierbarkeit von Pr?fungsergebnissen [4]. Um die inhaltliche Bedeutung der Zahlenwerte zu veranschaulichen, sei ein fiktives Beispiel vorangestellt. Ein Pr?fer habe einen hinreichend gro?en Fragenpool zur Verf?gung und beabsichtigt, die Abschlusspr?fung seines Fachgebiets mit 20 Fragen durchzuf?hren. Um eine Absch?tzung dar?ber zu gewinnen, ob die Fragenzahl f?r eine zuverl?ssige Pr?fung ausreicht, stellt er beim ersten Mal zwei Pr?fungen mit je 20 verschiedenen Fragen aus seinem Pool zusammen und setzt alle 40 Fragen bei 250 Studierenden ein. Danach bewertet der die beiden Pr?fungsteile unabh?ngig voneinander und vergleicht die dabei erzielten Noten.

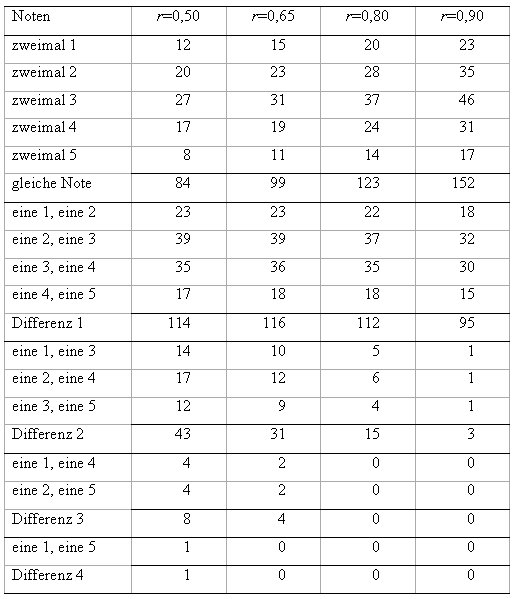
F?r die verschiedenen Reliabilit?tswerte 0,5, 0,65, 0,8 und 0,9 zeigt die Tabelle 4 [Tab. 4] die zu erwartenden H?ufigkeiten der Notenkombinationen.

(Dem Beispiel liegt folgendes Modell zu Grunde: Die Punktwerte sind bivariat normalverteilt mit Erwartungswerten 0 und Standardabweichungen 1 bei einer Korrelation von r . Als Notengrenzen sind f?r die beiden Pr?fungen jeweils die Werte x45 = -1, 28155, x34 = x45 +0, 8, x23 = x45 +1, 6 und x12 = x45 +2, 4 gew?hlt, so dass die Notenverteilung der beiden Pr?fungen f?r die Noten 1 - 5 etwa 13%, 24%, 31%, 22% und 10% ist. Dies entspricht einer realistischen Notenverteilung in einer Pr?fung. Die Erwartungswerte der Notenkombinationen ergeben sich aus der bivariaten Normalverteilung in Abh?ngigkeit von der Korrelation r.)

Aus der Tabelle 4 [Tab. 4] geht hervor, dass bei einer Reliabilit?t von 0,5 lediglich 84 der 250 Pr?flinge die gleiche Note erhalten, bei 114 Studierenden differieren die beiden Notenwerte um eine Stufe. W?hrend Notenunterschiede von einer Stufe noch nicht als gravierender Mangel angesehen werden brauchen, stellt die Tatsache, dass bei mehr als 20% der Pr?fungskandidaten ein Unterschied von mindestens zwei Notenstufen vorliegt, den Wert einer solchen Pr?fung und ihrer Benotung sicher in Frage. Besonders auffallend sind nat?rlich die F?lle, in denen einmal eine F?nf und einmal eine Note gleich oder sogar besser als Drei vergeben wird (17 Pr?flinge, entsprechend 6,8%). Eine zuverl?ssige Identifikation ungen?gend vorbereiteter Kandidaten ist mit einer solchen Pr?fung offensichtlich nicht m?glich.

Nun ist bei schriftlichen Pr?fungen eine Reliabilit?t von 0,5 oder niedriger unserer Erfahrung nach eher selten, die in der zweiten Spalte der Tabelle angegebenen Werte f?r eine Reliabilit?t von 0,65 sind in der Praxis jedoch durchaus h?ufig zu finden. Die Benotung ist hier schon deutlich stabiler, aber bei immer noch 35 Personen - das sind 14% der Studierenden - ist die Differenz der beiden Noten 2 oder 3.

In der Literatur wird f?r relevante Pr?fungen eine Mindestreliabilit?t von 0,8 angegeben, die dabei zu erwartenden Kombinationen sind in der dritten Spalte aufgef?hrt. Auch hier erh?lt noch nicht einmal die H?lfte der Personen die gleiche Note, der Anteil von Differenzen um zwei Notenstufen betr?gt noch 6%. H?here Differenzen treten nur noch mit einer zu vernachl?ssigenden Wahrscheinlichkeit auf. Erst ab einer Reliabilit?t von 0,9 steigt der Anteil von gleichen Noten auf mehr als 2/3 der Pr?flinge (siehe letzte Spalte der Tabelle 4 [Tab. 4]).

Bedenkt man die Bedeutung, die den Noten beigemessen werden und die Konsequenzen f?r den Studenten, der eine Pr?fung nicht besteht, so d?rfte der Mindestwert von 0,8, der allgemein f?r aussagekr?ftige Pr?fungen gefordert wird, sicherlich nicht zu niedrig angesetzt sein (jeder Pr?fungsersteller sollte f?r die in Tabelle 4 [Tab. 4] angegebenen Zahlenwerte ?berlegen, ob er seine eigenen Leistungen mit einem Test beurteilt wissen will, der die genannten G?teeigenschaften aufweist).

2. Formen der Reliabilit?t und interne Konsistenz

Um die Zuverl?ssigkeit einer Pr?fung festzustellen, w?re das Naheliegendste nat?rlich eine Pr?fungswiederholung. Das ist bei Lernstoffen jedoch nicht praktikabel, da sich die Pr?fungskandidaten an die einzelnen Aufgaben erinnern und die zugeh?rigen Antworten lernen (in anderen Zusammenh?ngen ist die Bestimmung einer solchen Re-Test-Reliabilit?t durchaus sinnvoll). Eine andere M?glichkeit besteht in der Konstruktion eines "Paralleltests", also einer Pr?fung, die die selben Pr?fungsinhalte, aber mit anderen Fragen oder Aufgaben enth?lt. Die Reliabilit?t ist dann die Korrelation der beiden Pr?fungsergebnisse. Hierzu sind keine zwei Pr?fungstermine notwendig, die Aufgaben der beiden Pr?fungen k?nnten direkt nacheinander oder ineinander verschr?nkt dargeboten werden (der fiktive Pr?fer im vorhergehenden Abschnitt hat diesen Weg gew?hlt). Praktisch ist dieser Weg zwar gangbar, erfordert aber eine entsprechende Konstruktion der Pr?fung mit genauer Definition der Pr?fungsziele und des -inhalts ("Blue-Print"). Ohne Paralleltestkonstruktion kann man die Pr?fung nach einem bestimmten vorgegebenen Schema (z. B. Pr?fung 1 besteht aus den ungeraden Pr?fungsfragen, Pr?fung 2 aus den geraden) oder nach Zufall in zwei H?lften teilen und die Korrelation der Ergebnisse der beiden H?lften bestimmen ("Split-Half-Reliabilit?t", meist werden die beiden Testh?lften als gleich gro? angenommen, was zwar gewisse Optimalit?tseigenschaften beinhaltet, jedoch nicht zwingend notwendig ist).

F?r die beiden Pr?fungsh?lften hat man je Kandidat zwei Pr?fungsergebnisse S 1 und S 2, die Split-Half-Reliabilit?t ist die Korrelation der beiden Werte und kann als Zuverl?ssigkeit der Pr?fung 1 wie auch der Pr?fung 2 interpretiert werden. F?r die Beurteilung der Kandidaten wird man die beiden Pr?fungspunktwerte S 1 und S 2 zusammenfassen, ob man die beiden Werte summiert oder mittelt, macht keinen Unterschied. Mathematisch l?sst sich unter relativ schwachen Modellannahmen zeigen, dass die Verwendung der zusammengefassten Punktzahl die Zuverl?ssigkeit erh?ht, die entsprechende Formel, mit der aus der Korrelation der beiden Einzelpr?fungen auf die Zuverl?ssigkeit der zusammengefassten geschlossen werden kann, ist als Spearman-Brown-Formel bekannt ([12], vgl. auch den n?chsten Abschnitt).

Es bleibt jetzt noch eine kleine Unsch?nheit im genannten Vorgehen zu behandeln: Die Aufteilung in zwei H?lften ist willk?rlich, bei einer anderen Aufteilung w?rde man auch einen anderen Wert f?r die Reliabilit?t erhalten. Abhilfe schafft hier Cronbachs α-Koeffizient (sog. interne Konsistenz)t: Bestimmt man - so wie im letzten Abschnitt angegeben - die Reliabilit?t des Gesamttests aus allen m?glichen Testhalbierungen, so ist dieser Mittelwert identisch mit α.

Eine Anmerkung ist noch vonn?ten: Die Reliabilit?t ist mathematisch nicht mit der internen Konsistenz identisch. In vielen Ver?ffentlichungen wird α mit der Reliabilit?t gleichgesetzt, dies ist falsch. Cronbachs α ist tats?chlich eine untere Grenze f?r die Reliabilit?t, d. h. es gilt allgemein α ≤ r. Die Reliabilit?t kann jedoch u. U. deutlich h?her als α sein. Die Verwendung besserer Absch?tzungen erfordert jedoch einen h?heren Aufwand und statistische Fachkenntnisse, f?r das hier angestrebte Ziel eines How-to-do einer einfachen Pr?fungsauswertung ist α in jedem Fall ad?quat, zumal man sich mit einem ausreichend hohen α auf der sicheren Seite befindet.

Zur praktischen Berechnung ist die Verwendung eines Statistik-Programmpakets wie z. B. SPSS, SAS oder das frei erh?ltliche R, dringend zu empfehlen, diese liefern neben der Reliabilit?t auch noch ein weiteres Ma? zur Beurteilung der einzelnen Aufgaben. Eine "gute" Aufgabe steuert Informationen zur Differenzierung der Pr?fungskandidaten bei, als einfaches Ma? dient dabei die Trennsch?rfe. Gleichzeitig dient sie zur Erh?hung der Messzuverl?ssigkeit, weshalb diese sinken sollte, wenn man die Aufgabe in der Pr?fung weggelassen h?tte. Umgekehrt d?rfte eine schlechte Aufgabe die Messzuverl?ssigkeit absinken lassen, ihre Herausnahme aus der Pr?fung w?rde die Zuverl?ssigkeit sogar erh?hen. Aus diesem Grund bestimmt man f?r jede Aufgabe die Zuverl?ssigkeit der restlichen Pr?fung, das "α if deleted". Als problematisch sind dann all die Aufgaben anzusehen, bei denen das "α if deleted" h?her ist als das α der Gesamtpr?fung, diese Aufgaben wirken reliabilit?tsmindernd (sofern man Cronbachs α als Reliabilit?tsma? verwendet, s. hierzu noch die Anmerkungen zur Reliabilit?t nicht-homogener Tests weiter unten) Praktisch stimmt dieses Kriterium mit dem der Trennsch?rfe nahezu ?berein, sollte der Vollst?ndigkeit halber jedoch mitbestimmt werden.

3. Erh?hung der Reliabilit?t von Pr?fungen

Wie bereits erw?hnt, wird in der Literatur ein Mindestwert von 0,8 f?r die Reliabilit?t angegeben. Die Praxis zeigt, dass dieser Wert jedoch bei vielen Pr?fungen unterschritten wird. Zun?chst sei bemerkt, dass - etwas vereinfachend - die Reliabilit?t mit den mittleren Korrelationen der Punktwerte der Aufgaben untereinander und der Anzahl der Aufgaben ansteigt. Damit sind auch die beiden M?glichkeiten angegeben, die Reliabilit?t von Pr?fungen zu steigern: Eine Verbesserung der Aufgabenqualit?t f?hrt meist zu deutlichen Erh?hungen der Interkorrelationen und dadurch zur Reliabilit?tssteigerung. Ein Beispiel f?r den Erfolg solcher Bem?hungen ist der kontinuierliche Anstieg der Zuverl?ssigkeiten der an der medizinischen Fakult?t Heidelberg durchgef?hrten OSCE-Pr?fungen, bei der die geforderte Mindestgrenze von 0,8 nahezu erreicht wurde [16].

Eine andere M?glichkeit zur Reliabilit?tserh?hung ist, mehr Aufgaben zu stellen. Dies st??t nat?rlich auf praktische Grenzen, so dass unseres Erachtens immer der Qualit?tsverbesserung der Aufgaben der Vorzug gegeben werden sollte. Um eine Absch?tzung zu gewinnen, wie sich eine Ver?nderung der Aufgabenzahl unter sonst gleichen Bedingungen auswirkt, ist nachstehende Formel hilfreich: Hat eine Pr?fung n Aufgaben und ist r n ihre Reliabilit?t, so ist

die entsprechende Reliabilit?t einer Pr?fung mit m Aufgaben (f?r m = 2 und n = 1 erh?lt man die oben erw?hnte Formel von Spearman-Brown). Durch Umstellen der Formel kann man aus rn und n die notwendige Fragenzahl m bei angezielter Reliabilit?t rm bestimmen:

Verwenden wir das am Anfang des Abschnitts angegebene Beispiel einer Pr?fung mit n = 20 und Reliabilit?t r n = 0, 5. Um eine Reliabilit?t von 0,8 zu erzielen, ben?tigt man

Aufgaben, will der Pr?fer eine Vervierfachung seiner Pr?fungsdauer vermeiden, muss er die Pr?fungsqualit?t erheblich erh?hen.

Nat?rlich ist es auch m?glich, "eine" Pr?fung an mehreren Terminen durchzuf?hren (z. B. vier Teilpr?fungen mit je 20 Aufgaben statt einer einzigen Abschlusspr?fung mit Aufgaben). Die Zuverl?ssigkeit der Gesamtbewertung zusammengefasster Teilpr?fungen bestimmt sich aus allen Einzelaufgaben.

Die Reliabilit?t kann als das quantitative Hauptkriterium einer Pr?fung angesehen werden, da sie angibt, wie zuverl?ssig die Pr?fungsergebnisse sind. Man wird einwenden, dass die Validit?t eigentlich das Hauptkriterium darstellen sollte. Hierf?r hat man aber bei Pr?fungen meist keine geeignete quantitative Absch?tzung, es kann i. A. nur eine hinl?ngliche Inhaltsvalidit?t ?ber eine repr?sentative Abdeckung der Lehrinhalte durch die Pr?fungsfragen gesichert werden (siehe weiter unten), dennoch k?nnen empirisch nicht belegbare Spekulationen ?ber die Validit?t einer Pr?fung eine mangelhafte Messzuverl?ssigkeit nicht heilen.

Auf ein damit zusammenh?ngendes Problem sollte noch hingewiesen werden: Pr?fungen dienen nicht allein dazu, zuverl?ssig Unterschiede zwischen Studierenden zu quantifizieren, sie sollen und m?ssen auch das f?r das Fach notwendige Basiswissen und die grundlegenden Fertigkeiten abpr?fen. Eine gute Lehre wird diese auch erfolgreich vermitteln und dann werden auch die meisten Studierenden die grundlegenden Kenntnisse beherrschen und die entsprechenden Aufgaben erfolgreich bearbeiten. Solche Aufgaben weisen aber schlechte Kennwerte auf: Sie sind viel zu leicht, besitzen nur eine geringe Trennsch?rfe und vermindern die interne Konsistenz der Pr?fung (man beachte: sie verringern nicht die Reliabilit?t, steigern sie aber auch nicht). Daraus folgt, dass die oben beschriebenen G?tema?e nicht alleiniges Kriterium f?r die Auswahl von Aufgaben sein k?nnen; das Ziel einer hohen Reliabilit?t darf nicht dazu f?hren, eine fachlich inad?quate Pr?fung durchzuf?hren (Stichwort "Kolibri-Fragen"). Jeder Pr?fer sollte aber wissen, welche Aufgaben "schlecht" im Sinne der klassischen Testtheorie sind und, - wenn Aufgaben mit unzureichenden G?tema?en in Pr?fungen eingesetzt werden - gute Gr?nde f?r ihre Verwendung nennen k?nnen (siehe hierzu auch "… und was ist mit der Validit?t" weiter unten).

Zusammenfassung

Nachfolgend sind die einzelnen Schritte der hier vorgestellten quantitativen Pr?fungsbeurteilung zusammen gefasst (Tabelle 5 [Tab. 5] enth?lt noch einmal alle zu ber?cksichtigenden Kennwerte)

• 1. Ergebnis?bersicht
• 1.1 H?ufigkeitstabelle der Punktwerte und Noten
• 1.2 Histogramm der Punktwerte
• 1.3 Identifikation von Ausrei?ern
• 2. Teststatistische Analyse der Aufgaben
• 2.1 Berechnung der Aufgabenschwierigkeiten P
• (mit graphischer Darstellung der P )
• 2.2 Berechnung der Trennsch?rfeindizes D', r', der Aufgaben
• (mit graphische Darstellung der Schwierigkeiten in den Untergruppen gut/mittel/schlecht)
• 2.3 Histogramme der Aufgabenschwierigkeiten P und Trennsch?rfen r'
• 3. Einzelantwort-/Distraktoranalyse (sofern sinnvoll)
• 3.1 Bestimmung der H?ufigkeiten der Einzelantworten
• (mit graphischer Darstellung)
• 3.2 Bestimmung der Diskrimination der Einzelantworten r' und D'
• (mit graphischer Darstellung in den Untergruppen)
• 4. Reliabilit?t
• 4.1 Bestimmung von Cronbachs α (nach Ausschluss von Ausrei?en)
• 4.2 Bestimmung von "α if deleted" f?r jede Aufgabe
• 4.3 Berechnung der notwendigen Zahl m0.8 von Pr?fungsfragen f?r Mindestreliabilit?t 0,8.

Nach der in Schritt 1 erfolgenden ?bersicht ?ber die Pr?fungsresultate, die auch einer weiteren Kontrolle der Bewertung dient, liefern die Schritte 2 und 3 die empirische Basis f?r die Revision von Aufgaben und Pr?fungszusammenstellung. Revisionsbed?rftig sind zu leichte, zu schwere oder wenig trennscharfe Aufgaben. Diese Analyseschritte sollten vor Bekanntgabe der Pr?fungsergebnisse erfolgen, da hier problematische Aufgaben (unklare Aufgabenstellungen, mehrdeutige oder sogar fehlerhaften Antwortm?glichkeiten) meist auffallen und bei der Korrektur ber?cksichtigt werden k?nnen. Dies ist in jedem Fall besser als die nachtr?gliche Ber?cksichtigung gerechtfertigter Einspr?che von Studenten gegen Pr?fungsaufgaben.

Der abschlie?ende Schritt 4 dient zur Kontrolle der Zuverl?ssigkeit der Pr?fung; bei ungen?gender Reliabilit?t muss eine Verbesserung der Aufgabenqualit?t und/oder Vergr??erung der Aufgabenanzahl erfolgen, was nat?rlich erst bei den folgenden Pr?fungen zum Tragen kommt (s. "Erh?hung der Reliabilit?t von Pr?fungen").

Wichtig f?r die Praxis ist eine kompakte Darstellung der Ergebnisse der Aufgabenauswertung, die Standardausgaben von Programmpaketen sind meist zu "unhandlich" und zu umfangreich. Es ist einigerma?en m?hsam, sich bei der Betrachtung der Ergebnisse durch Dutzende Seiten Papier oder Bildschirmdarstellungen durchzuarbeiten.

Unserer Erfahrung nach hat sich bei der Standardauswertung f?r den ersten Schritt eine einfache tabellarische Darstellung bew?hrt, in der je Aufgabe die Kennwerte P, D', r', und "α if deleted" sowie ein „Warnhinweis" aufgef?hrt werden. Gewarnt wird bei zu schweren oder sehr leichten Aufgaben (P < 0,4 bzw. P > 0,85) und bei zu geringer Trennsch?rfe (r' < 0,2) sowie diskrepanten Trennsch?rfen |r' - | > 0,2. Damit lassen sich bei einer Pr?fung mit 60 Aufgaben die wesentlichen Ergebnisse leicht auf zwei Seiten darstellen. Im zweiten Schritt werden nur f?r die problematischen Aufgaben die Details betrachtet (hier erweisen sich die graphischen Darstellungen als sehr hilfreich, nur f?r eingefleischte Zahlenliebhaber sind diese platzbed?rftigeren Darstellungen ?berfl?ssig).

?hnlich geht man bei der Einzelantwort-/Distraktorenanalyse vor, die umfangreicheren Darstellungen werden nur bei den Aufgaben verwendet, die hinsichtlich der H?ufigkeiten oder Trennsch?rfen kritisch sind.

Nat?rlich gibt es hier bei den Pr?fern auch unterschiedliche Vorlieben, manche bevorzugen auch bereits im ersten Schritt die graphischen Varianten der Tabellen 2 und 3 [Tab. 2] [Tab. 3].

Anmerkung

Zu den klassischen G?tekriterien z?hlen neben der Reliabilit?t noch Objektivit?t und Validit?t. Da hier im Wesentlichen die quantitative Auswertung von Pr?fungsdaten thematisiert ist, sollen hier nur einige Anmerkungen angef?gt werden, bei den standardm??ig durchgef?hrten Pr?fungen liegen n?mlich weder f?r Objektivit?t noch Validit?t ?berhaupt empirische Daten vor.

1. Objektivit?t

Bei der Objektivit?t unterscheidet man ?blicherweise Durchf?hrungs-, Auswertungs- und Interpretationsobjektivit?t. Erstere l?sst sich durch eine hinreichende Standardisierung des Pr?fungsablaufs gew?hrleisten, bei schriftlichen Klausuren ist diese ?blicherweise gegeben, f?r m?ndliche und praktische Pr?fungen ist eine gen?gende Durchf?hrungsobjektivit?t bei OSPE/OSCE, OSLER, strukturierten m?ndlichen Pr?fungen u. a. Pr?fungsformaten zu sichern. Kritischer ist die Auswertungsobjektivit?t, bei der bei Pr?fungen noch zwischen der Objektivit?t der Leistungsfeststellung und der der -beurteilung zu unterscheiden ist. Zu deren Sicherung sollte - soweit logistisch und personell m?glich - wenigstens eine stichprobenartige ?berpr?fung durch den Einsatz voneinander unabh?ngiger Bewerter (Korrektoren oder Pr?fern) erfolgen.

2. . . und was ist mit der Validit?t?

Die Reliabilit?t gibt nur an, wie genau die Ergebnisse sind, nicht jedoch, ob das was gemessen wird, auch das ist, was man ?berhaupt messen will. Bekannt ist hierzu die Diskussion um den Stellenwert von Multiple-Choice-Klausuren, da sich bei diesen die Frage stellt, inwieweit damit wirklich die f?r die ?rztliche T?tigkeit notwendigen Kenntnisse in einem medizinischen Teilgebiet gemessen werden oder schlicht nur die mittelfristige Merkf?higkeit der Studierenden.

Wenn dem so ist, f?hren dann Bem?hungen zur Reliabilit?tssteigerung nicht windschief an der eigentlichen Zielsetzung der Pr?fung medizinischer Kenntnisse und Fertigkeiten vorbei? Richtig an dieser kritischen Frage ist, dass nat?rlich das wesentliche Ziel "guter Pr?fungen" eine m?glichst hohe Validit?t ist, andererseits ist die Reliabilit?t eine notwendige Bedingung, um mit einer Pr?fung ?berhaupt etwas zu erfassen (eine Pr?fung die nicht reliabel ist, ist auch nicht valide!).

Das Problem der Validit?t besteht darin, objektive und nachpr?fbare Au?enkriterien zur Validit?tspr?fung anzugeben (externe oder Kriterienvalidit?t, "Gold-Standard"), weshalb als Validit?tskonzept in der Forschung die Konstruktvalidit?t in den Vordergrund getreten ist. (vgl. [8] [15] und speziell in Bezug auf medizinische Pr?fungen [6], [19], [21]).

(In der Literatur finden sich neben den Begriffen der Kriterien- (externen) und Konstruktvalidit?t auch noch etwa die Augenschein- ("face-validity") und die Kontent- oder Inhaltsvalidit?t. Beide Begriffe sind auf Grund ihres subjektiven Charakters lediglich als heuristische Kriterien verwendbar, f?r eine wissenschaftliche Argumentation jedoch kaum von Nutzen.)

Hierzu sind f?r medizinische Pr?fungen und deren Aussagekraft f?r praktische ?rztliche T?tigkeiten eine Reihe von Untersuchungen ver?ffentlicht worden (Reviews der Literatur finden sich etwa in [9], [14], [20]), die einerseits durchaus deren Validit?t belegen, andererseits aber zeigen, dass Pr?fungsformen nicht per se eine h?here oder geringere Aussagekraft aufweisen, sondern die Qualit?t der einzelnen Pr?fungen ausschlaggebend ist und erst eine Kombination der Ergebnisse verschiedener Pr?fungsformate (f?r theoretisches Wissen, praktische Fertigkeiten usw.: "Triangulation") eine hohe Validit?t sicher stellen kann (vgl. z. B. [1]).

Die empirische ?berpr?fung der Validit?t kann nicht Aufgabe der einzelnen Pr?fungsersteller sein, diese muss einer fundierten Pr?fungsforschung vorbehalten bleiben. Dem Pr?fer obliegt es, durch eine sorgf?ltige Aufgabenauswahl (Vermeidung von Konstruktunterrepr?sentation durch eine hinreichend breite und repr?sentative inhaltliche Abdeckung des Themengebiets und Vermeidung von konstruktirrelevanter Varianz durch Klarheit der Aufgabenstellungen) und der Sicherung von Objektivit?t und Reliabilit?t die wesentlichen Voraussetzungen einer validen Pr?fung zu schaffen (vgl. [3], [5]).

3. Reliabilit?t nicht-homogener Tests

Die Ausf?hrungen zur Reliabilit?t basieren auf mathematisch relativ einfachen Annahmen, die jedoch bei Pr?fungen in der Medizin nicht erf?llt zu sein brauchen. Insbesondere ist die Homogenit?t der Pr?fung kaum anzunehmen (d. i. die Annahme, dass die abzupr?fende Fertigkeit nur eindimensional ist, und sich nicht in Unterdimensionen aufspalten l?sst - wie z .B. bei der Intelligenz in sprachliche, logische und weitere Intelligenzfaktoren).

Bei nicht-homogenen Tests kann die Absch?tzung der Reliabilit?t mittels Cronbachs α zu einer deutlichen Untersch?tzung f?hren. Viele Bef?rworter von praktischen Pr?fungen f?hren deren h?here Inhaltsvalidit?t ins Feld und stufen die Bedeutung der Reliabilit?t deshalb herab, dabei ist jedoch zu fragen, ob sie tats?chlich die Reliabilit?t meinen oder Cronbachs α, also die interne Konsistenz. Verwechselt werden beide Begriffe deshalb, weil in der Mehrzahl aller praxisorientierten Ver?ffentlichungen α mit der Reliabilit?t gleichgesetzt wird, was nur unter bestimmten Voraussetzungen zutrifft, im Allgemeinen jedoch definitiv falsch ist.

Auswertungsverfahren, die die Nicht-Homogenit?t von Pr?fungen ber?cksichtigen, sind z. B. faktorenanalytische Verfahren (vgl. z. B. [13]). Die Anwendung dieser Methoden erfordert jedoch eine hinreichende statistische oder biometrische Fachkompetenz und ist mit einem nicht unerheblichen Zeitaufwand verbunden, ein einfaches "How-to-do", wie es die vorliegende Arbeit f?r die basale Pr?fungsauswertung darstellt, kann beim augenblicklichen Kenntnisstand ?ber die Struktur medizinischer Pr?fungen nicht erstellt werden.

Fazit

Zum Abschluss sollte noch einmal betont werden, dass die beschriebenen Auswertungen keinen Selbstzweck darstellen, sondern die objektive und empirisch fundierte Basis einer kontinuierlichen Entwicklung und Verbesserung medizinischer Pr?fungen darstellen, die immer in engem Zusammenhang mit der Festlegung und der Vermittlung von Lehrinhalten stehen muss.

Eine wesentliche Aufgabe f?r die Zukunft ist die Etablierung einer medizinischen Pr?fungsforschung, die nat?rlich methodisch ?ber die dargestellten Verfahren hinausgehen muss und in Zusammenarbeit mit Einzelpr?fern und Pr?fungsverb?nden eine Sicherung der Validit?t medizinischer Pr?fungen zum Ziel hat.

Danksagung

Wir danken allen Kolleginnen und Kollegen des Kompetenzzentrums f?r Pr?fungen in der Medizin sowie Herrn Prof. H. Geiss f?r die konstruktive Hilfe bei der Erstellung des Manuskripts.

---

Literatur

[1] Auewarakul C, Downing SM, Jaturatamrong U, Praditsuwan R. Sources of validity evidence for an internal medicine student evaluation system: an evaluative study of assessment methods. Med Educ. 2005;39:276-283.
[2] Bloch R, Hofer D, Krebs R, Schl?ppi P, Weis S, Westk?mper R. Kompetent pr?fen. Handbuch zur Planung, Durchf?hrung und Auswertung von Facharztpr?fungen. Medizinische Fakult?t Universit?t Bern, Bern/Wien: Institut f?r Aus-, Weiter- und Fortbildung; 1999.
[3] Downing SM, Haladyna TM. Validity threats: overcoming interference with proposed interpretations of assessment data. Med Educ. 2004;38:327-333.
[4] Downing SM. Reliability: on the reproducibility of assessment data. Med Educ. 2004;38:1006-1012.
[5] Downing SM. Threats to the validity of clinical teaching assessments: what about rater error? Med Educ. 2005;39:353-355.
[6] Downing SM. Validity: On the meaningful interpretation of assessment data. Med Educ. 2003;37:830-837.
[7] Ebel RL, Frisbie DA. Essentials of educational measurement. Englewood Cliffs, N.J.: Prentice Hall; 1991.
[8] Grotjahn R. Testtheorie: Grundz?ge und Anwendungen in der Praxis. In: Wolff A, Tanzer H (Hrsg.), Materialien Deutsch als Fremdsprache (Bd. 53). Regensburg: FaDaF. 2000:S.304-341.
[9] Hutchinson L, Aitken P, Hayes T. Are medical postgraduate certification processes valid? A systematic review of the published evidence. Med Educ. 2002;36:73-91.
[10] Kelley TL. The selection of upper and lower groups for the validation of test items. J Educ Psych. 1939;30:17-24.
[11] Lienert GA, Raatz A. Testaufbau und Testanalyse. Weinheim: Beltz; 1994.
[12] Lord FM, Novick MR. Statistical theory of mental test scores. Reading: Addison-Wesley; 1968.
[13] Lucke JF. The a and of congeneric test theorie: An extension of reliability and internal consistency to heterogeneous tests. Appl Psych Meas. 2005;29:65-81.
[14] Lynch DC, Surdyk PM, Eiser AR. Assessing professionalism: a review of the literature. Med Teach. 2004;26:366-373.
[15] Messick S. Validity. In: Linn RL (Hrsg.) Educational Measurement. New York: American Council of Education/McMillan Publishing Company. 1989:S13-103.
[16] Nikendei C, J?nger J. OSCE - praktische Tipps zur Implementierung einer klinisch-praktischen Pr?fung. GMS Z Med Ausbild. 2006;23(3):Doc.46.
[17] Rousseeuw PJ, Leroy AM. Robust Regression and Outlier Detection. New York: John Wiley & Sons Inc; 1987.
[18] Schulze J, Drolshagen S, N?rnberger F, Siegers CP, Syed ALI S. Pr?fen und Pr?fungen nach der neuen Approbationsordnung - Grunds?tze und Rahmenbedingungen. Med Ausbild. 2004;21:30-34.
[19] Van der Vleuten C, Schuwirth L. Assessing professional competence: from methods to programmes. Med Educ. 2005;39:309-317.
[20] Veloski JJ, Fields SK, Boex JR, Blank LL (2005). Measuring professionalism: a review of studies with instruments reported in the literature between 1982 and 2002. Acad Med. 2005;80:366-370.
[21] Wass V, Van der Vleuten C, Shatzer J, Jones R. Assessment of clinical competence. Lancet. 2001;357:945-949.